概念题

数据挖掘统计限制–没有免费午餐，哈希函数（第1章）

没有免费午餐定理(No Free Lunch，简称NFL)是wolpert和Macerday提出的“最优化理论的发展”之一。

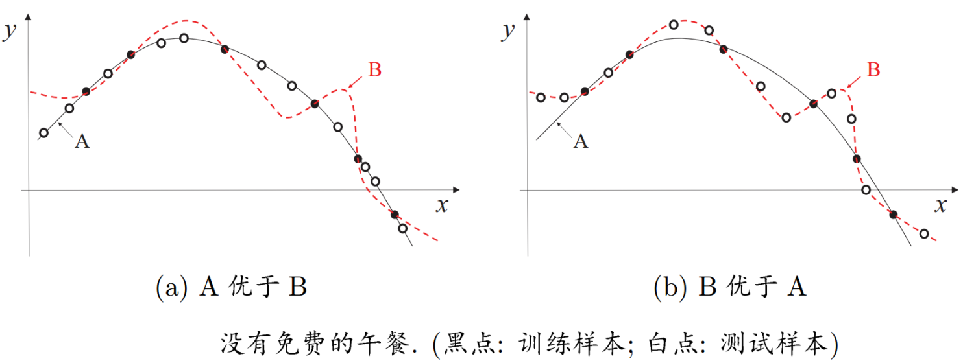
在机器学习算法中的体现为在没有实际背景下，没有一种算法比随机胡猜的效果好。

即没有一种算法在所有可能的问题上表现优于其他算法。

哈希函数

Hash，一般翻译做散列、杂凑，或音译为哈希，是把任意长度的输入（又叫做哈希键）通过哈希算法变换成固定长度的输出，该输出是桶编号。这种转换是一种压缩映射，桶编号的空间通常远小于哈希键的空间，不同的哈希键可能会哈希成相同的输出，所以不可能从桶编号来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。

hash函数的输入和输出

$h(s)=x\ mod\ B$

x表示哈希键，输出的h(s)为桶编号，桶的个数为整数B

例题：

哈希函数定义： h(X)=Xmod B 其中 X 是输入的整数，B=10

X=12345：12345%10=5，输出：5

X=abc ：97 + 98 + 99 = 294，294%10=4，输出：4

MapReduce概念，MapReduce适用和不适用场景（第2章）

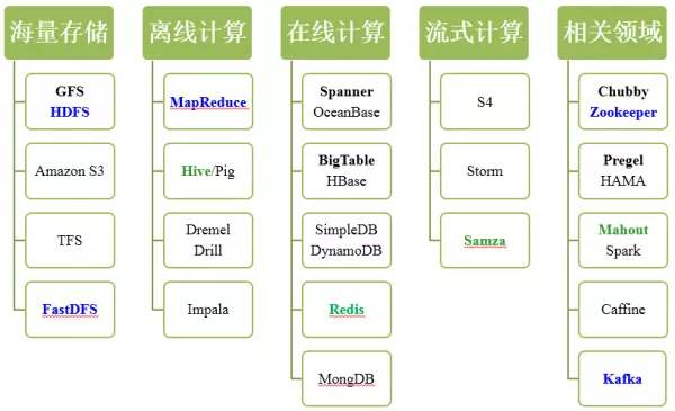
MapReduce是一种分布式的计算模式，用于大规模数据集的并行计算

Google和Hadoop系统都可以实现（Hadoop：Java）

抽象模型：Map 和 Reduce

统一框架：程序员不用关心系统细节

主要思想：分而治之用于搜索领域，解决海量数据的计算问题

MapReduce适用和不适用场景:

什么样的计算问题可以由MapReduce解决？需要离线计算的、大规模的矩阵乘法

最小哈希和文档相似性，距离的定义和性质（第3章）

最小哈希 minhashing

可以看成是一个特征提取的过程。集合的签名由大量计算(比如数百次)的结果组成，而每次计算是特征矩阵的最小哈希(minhashing)过程选择行的一个排列转换。任意一列的最小哈希值是在排列转换后的行排列次序下第一个列值为1的行的行号。每个排列转换定义了一个最小哈希函数h。

如何定义文档的相似：

字面上的相似：Jaccard 相似度

意义上的相似？（错误的）

字面上的相似度：完全重复、大部分文本重复

文档相似性的作用：

抄袭文档
镜像页面
同源新闻稿

欧式距离、曼哈顿距离:

Jaccard距离: D(x,y)= 1-SIM(x,y)

编辑距离:适用于字符串比较，两个字符串x, y的编辑距离等于将x转换为y所需要的单字符插入及删除操作的最小数目。

汉明距离:定义为两个向量中不同分量的个数。例如：10101和11110的距离是3

流数据特征和计算，数据采集系统架构（第4章）

流数据具有如下特征：

数据快速持续到达，潜在大小也许是无穷无尽的
数据来源众多，格式复杂
数据量大，但是不十分关注存储，一旦经过处理，要么被丢弃，要么被归档存储
注重数据的整体价值，不过分关注个别数据
数据顺序颠倒，或者不完整，系统无法控制将要处理的新到达的数据元素的顺序

流计算：实时获取来自不同数据源的海量数据，经过实时分析处理，获得有价值的信息

流计算秉承一个基本理念，即数据的价值随着时间的流逝而降低，如用户点击流。因此，当事件出现时就应该立即进行处理，而不是缓存起来进行批量处理。为了及时处理流数据，就需要一个低延迟、可扩展、高可靠的处理引擎

数据采集系统架构：

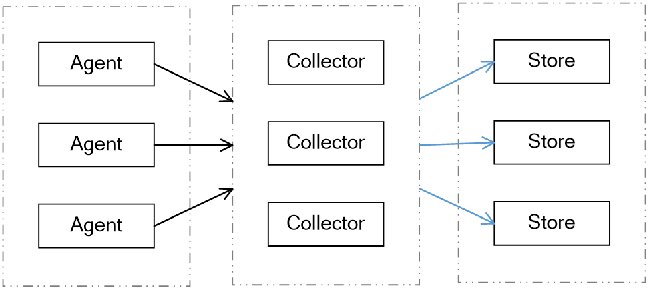
数据采集系统的基本架构一般有以下三个部分：

Agent：主动采集数据，并把数据推送到Collector部分

Collector：接收多个Agent的数据，并实现有序、可靠、高性能的转发

Store：存储Collector转发过来的数据（对于流计算不存储数据）

Web结构及其相应功能，抽税法理解，垃圾农场架构（第5章）

Web结构及其相应功能：

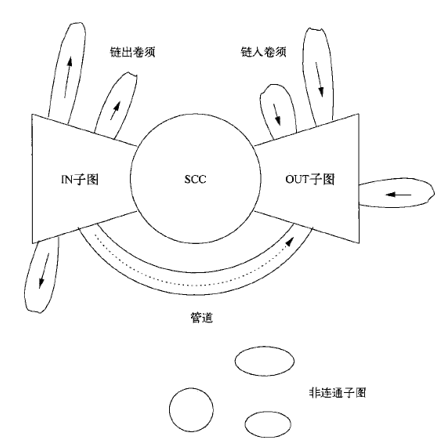
IN子图(in-component)：它由能够随着链接到达SCC但是从SCC却不能到达的网页组成。

OUT子图(out-component):它由SCC能够到达但是不能到达SCC的网页组成。

卷须子图(tendril) ：包括两种类型。一些卷须子图由可以从IN子图到达但不能到达IN子图的网页组成；另一些卷须子图由可以到达OUT子图但不能从OUT子图到达的网页组成。
管道(tube)由IN子图可达并可达OUT子图但是无法到达SCC或从SCC可达的网页组成。

管道（tube）：由IN直接到OUT的网页组成

孤立子图(isolated component):由整个图中从大的子图(SCC 、IN子图和OUT子图)无法到达，也无法到达大子图的网页组成。

抽税法：

$v'=\beta M {v} + (1 - \beta) \frac{e}{n} \\ v''=\beta M {v'} + (1 - \beta) \frac{e}{n} \\ ......$

随着迭代的进行，随机冲浪者在任何网页出现的概率都为0

我们可以修改随机冲浪者在Web上的冲浪过程。这种称为“抽税”的方法也能解决采集器陷阱的问题

抽税途径：我们对PageRank的计算进行少许修改，即允许每个随机冲浪者能够以一个较小的概率 $1-\beta$ 随机跳转(teleport)到一个随机网页，而不一定要沿着当前网页的出链前进。（抽税含义）

$βMv$ :随机冲浪者以 $β$ 继续向前走( $β$ 常数 0.8-0.9)

$(1- β)e/n$ 代表一个新的随机冲浪者以 $(1- β)$ 的概率随机选择一个网页进行访问。

垃圾农场架构：

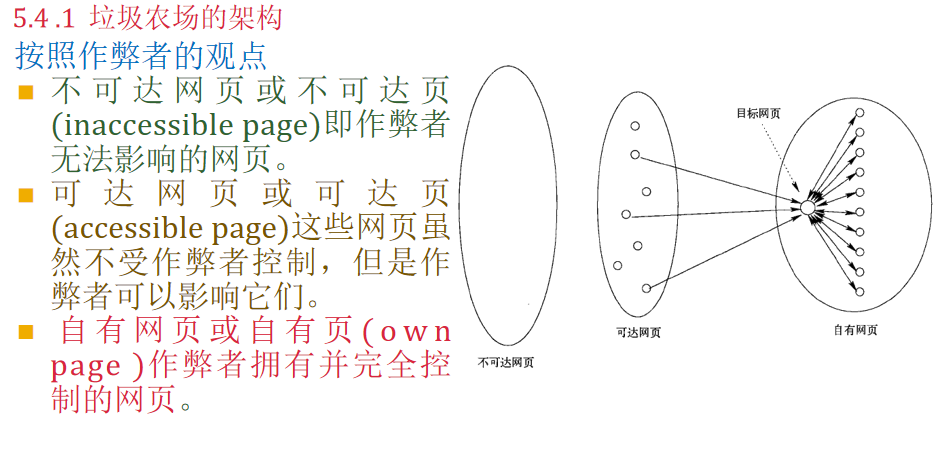
关联规则–支持度、可信度、兴趣度，最大频繁项集（第6章）

关联规则，可信度，兴趣度

l 抽取结果往往采用if-then形式的规则集合来表示，这些规则称为关联规则。

l 一条关联规则的形式为I→j ,其中I是一个项集，而j是一个项。该关联规则的意义是，如果I中所有项出现在某个购物篮的话，那么j“有可能”也出现在这一购物篮。

l 规则I →j的可信度=集合**I∪{j}**的支持度与I的支持度的比值，也就是，所有包含I的购物篮中同时包含j的购物篮的比例

l 定义 A → j的兴趣度 = Confidence(A→j)-Support(j)。当这个值很高或者是绝对值很大的负值都是具有意义的。前者意味着购物篮中A的存在在某种程度上促进了j的存在。后者意味着A的存在会抑制j的存在。

直观上看，一个在多个购物篮中出现的项集称为“频繁”项集。公式上，如果I是一个项集，I的支持度是指包含I (即I是购物篮中项集的子集)的购物篮数目。**假定有个支持度阈值S，如果I的支持度不小于S，则称I是频繁项集。**注意：需要提前定义支持度阈值S，I是一个集合。

最大频繁项集（Maximal Frequent Itemset, MFI）：一个频繁项集，如果它的任何超集都不是频繁项集，那么这个频繁项集就是最大频繁项集。换句话说，最大频繁项集是那些不能再扩展而仍然保持频繁的频繁项集。

假设有一个交易数据库，其中包含以下交易记录：

交易ID	项目集合
1	{A, B, C}
2	{A, B}
3	{A, C}
4	{B, C}
5	{A, B, C, D}

设定最小支持度阈值为2，即项集至少需要在2个交易记录中出现。假设置信度阈值为70%

在这个示例中，以下是一些频繁项集：

{A, B}，支持度为3
{A, C}，支持度为3
{B, C}，支持度为3
{A, B, C}，支持度为2

通过分析可以发现，{A, B, C} 是一个最大频繁项集，因为没有任何一个超集（如 {A, B, C, D}）是频繁的。

对于关联规则P（A—>B）=P(AB)/P(A)=3/4 > 70% 所以这个关联规则是可信的。

那对于P（AB—>C）=P(ABC)/P(AB)=2/3 < 70% 那么这个关联规则不可信。

举例：

$置信度Confidence(A→C)=\frac{AC出现的次数}{A出现的次数}=\frac{3}{4}$

$兴趣度Interest(A→C)=Confidence(A→C)-Support(C)=-0.05$

聚类的定义、影响因素和特点，聚类策略，K-means的初始条件（第7章）

聚类是对点集进行考察并按照某种距离测度将他们聚成多个“簇”的过程。

同一组内相似性较高，不同组相似性的点相似性低

1.聚类结果因任务不同而不同

2.聚类的结果取决于性能度量和距离计算的选择

按照聚类算法基本策略划分：

层次（凝聚式）算法：这类算法一开始将每个点都看成一个簇。簇与簇之间按照**接近度(closeness)**来组合，而接近度可以基于“接近”的不同含义采用不同的定义。当进一步的组合导致多个原因之一下的非期望结果时，上述组合过程结束。

点分配算法：即按照某个顺序依次考虑每个点，并将它分配到最适合的簇中。该过程通常都有一个短暂的初始簇估计阶段。一些变形算法允许临时的簇合并或分裂过程，或者当点为离群点(离当前任何簇的距离都很远的点)时允许不将该点分配到任何簇中。

k-means初始条件：如何选择初始中心点？

选择极有可能处于不同簇的点作为初始簇

（1）选择彼此相距尽可能远的点

（2）采用层次聚类，输出k个簇，在每个簇中选择离这个簇质心最近的那个点

web广告的分类（第8章）

广告信息平台（直投投放广告）：58同城，赶集网，安居客

媒体网站广告（展示广告）：同一个用户相邻两次访问，显示的广告不同

站内推荐：还买了什么，猜你喜欢

Adwords广告（搜索广告）：搜索引擎广告

计算题

Jaccard相似度计算

$SIM(S,T)=\frac{|S \cap T|}{|S\cup T|}$

例题1：2个集合A{1,2,3,4}、B{2,3,5,7}

SIM(A,B)=2/6=1/3

例题2：2个包A {a,a,a,b}、B{a,a,b,b,c}

SIM(A,B)=3/9=1/3

K-shingle计算（中文要会计算）

例题1：

D:{abcdabd} k=2 求k-shingle组成的集合

从左往右连着的k个字符分别是 ab bc cd da ab bd

ab出现2次，在集合里面只写一个

2-shingle组成集合为{ab,bc,cd,da,bd}

中文shingle：

k-shinger计算中文是不是一个中文和一个字母一样啊？是的。

示例：待分词的文本：公安人员在火车站台独自强守着岗位。

一般的分词：公安|人员|在|火车|站台|独自|强|守|着|岗位

IKAnalyzer：公安|公安人员|人员|在|火车|火车站|站台|独自| 自强|守着|岗位

ICTCLAS：公安人员｜在｜火车站｜站台｜独自｜强守｜着｜岗位

最小hash签名会计算，会分析哪些是真正的hash排列转换，会计算近似度的真实值和估计值

例题：

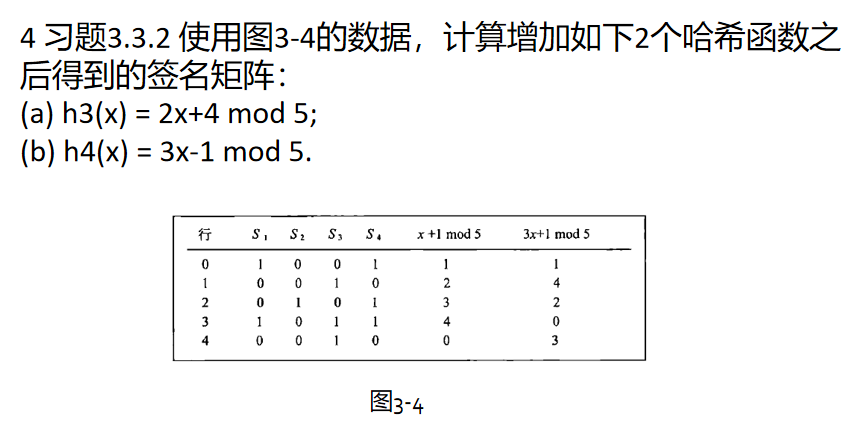
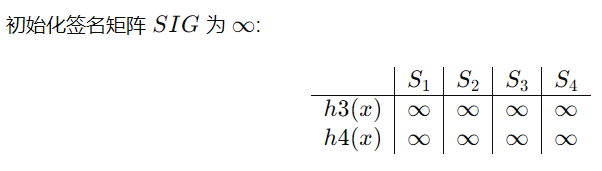
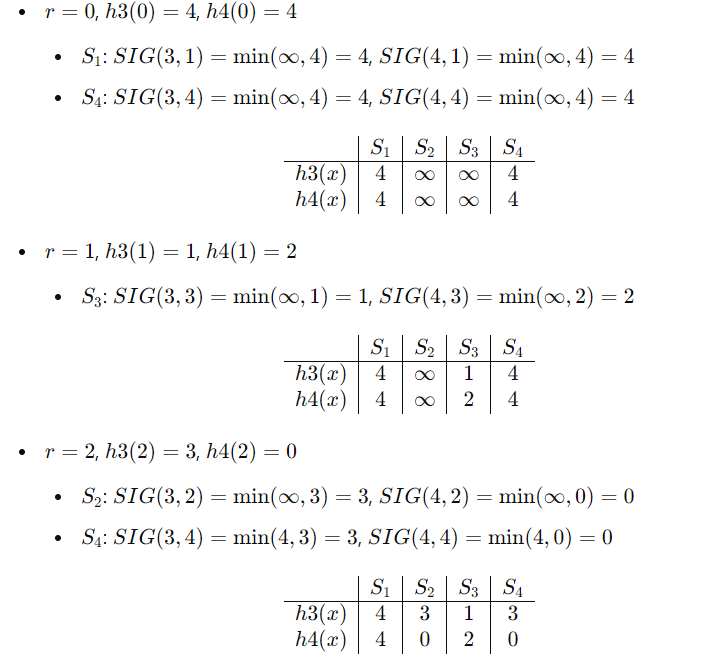
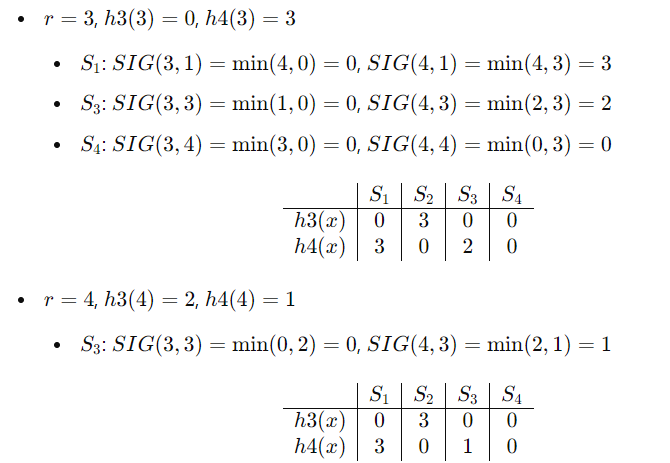
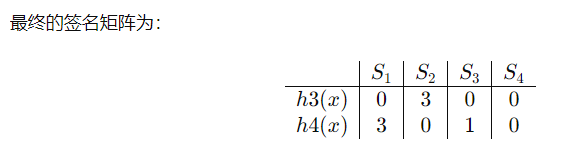
估计值SIM(S1,S4)=1/2

但S1.S4真实的Jaccard为：

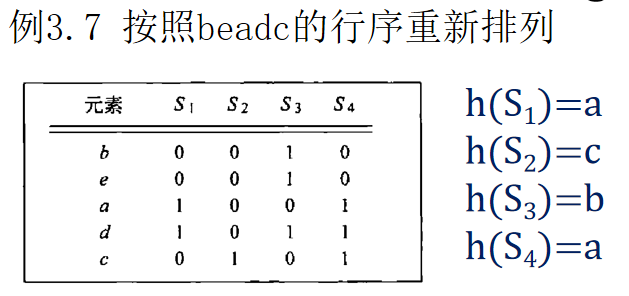
AMS算法，二阶矩原始计算

选出位置的那个元素x要计入value中，也就是从x.value=1开始计，看x往后的流中x再出现几次就在x.value加几。如第三个位置的c，后面有2个c，x1.value=1+2=3

PageRank（基本，主题）定义和迭代计算

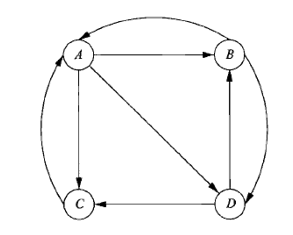
先做转移矩阵：

第一步列表:

源网页	出度	目标网页
A	3	BCD
B	2	AD
C	1	A
D	2	BC

第二步写转移矩阵:

$\ M = \begin{bmatrix} 0 & \frac{1}{2} & 1 & 0 \\ \frac{1}{3} & 0 & 0 & \frac{1}{2} \\ \frac{1}{3} & 0 & 0 & \frac{1}{2} \\ \frac{1}{3} & \frac{1}{2} & 0 & 0 \end{bmatrix} \$

$v' = \beta Mv + (1 - \beta) \frac{e}{n}$

假设初始状态概率向量：

$\ v= \begin{bmatrix} \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \end{bmatrix} \$

假设 $\beta=0.8$

则

$v'=\beta M {v} + (1 - \beta) \frac{e}{n}=\begin{bmatrix} \frac{21}{60} \\ \frac{13}{60} \\ \frac{13}{60} \\ \frac{13}{60} \end{bmatrix} \$

然后迭代

$v''=\beta M {v'} + (1 - \beta) \frac{e}{n} \\ v'''=\beta M {v''} + (1 - \beta) \frac{e}{n} \\ ......$

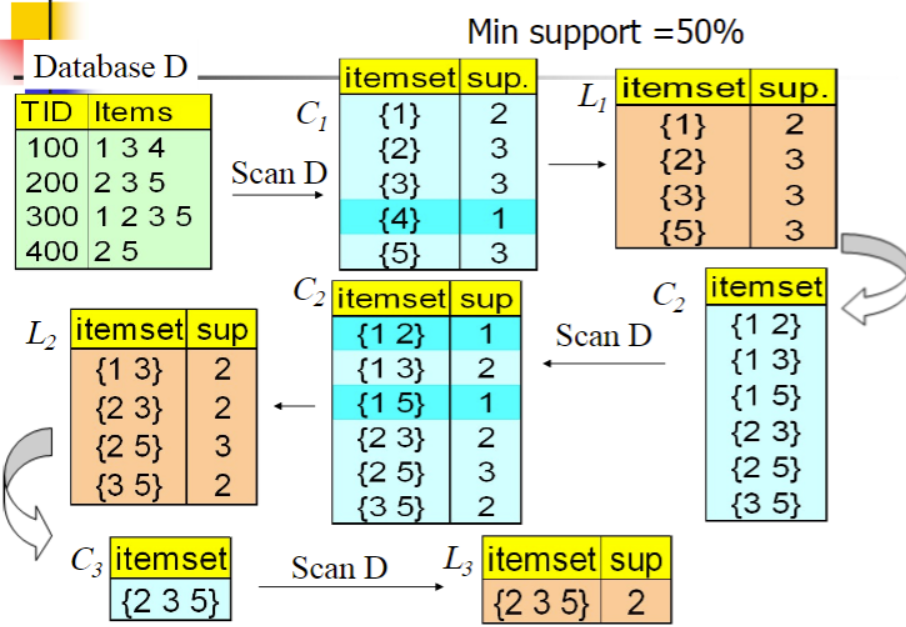
A-priori的计算

K-means(均值) 聚类计算

1
2
3

(4, 10), (4, 8), (7, 10), (6, 8), (3, 4), (10, 5), 
(12, 6), (11, 4), (12, 3), (9, 3), (5, 2), (2, 2)

计算每个点到三个中心点的距离，并将其分配到最近的中心点：

簇1的点：C1：(4, 10), (4, 8), (7, 10), (6, 8)
簇2的点：C2：(10, 5), (12, 6), (11, 4), (12, 3), (9, 3)
簇3的点：C3：(3, 4), (5, 2), (2, 2)

重新计算中心点

簇1 （ $\frac{21}{4}$ , $\frac{36}{4}$ ）

簇2 （ $\frac{54}{5}$ , $\frac{21}{5}$ ）

簇3 （ $\frac{10}{3}$ , $\frac{8}{3}$ ）

1从数据集中随机选取K个对象，作为K个簇的初始聚类中心；

2计算剩下的对象到K个簇中心的相似度，将这些对象分别划分到相似度最高的簇；

3根据聚类结果，更新K个簇的中心，计算方法是取簇中所有对象各自维度的算术平均值；

4将数据集中全部元素按照新的中心重新聚类；达到算法停止条件，转至步骤6；

5否则转至步骤3；

6输出聚类结果。

南京邮电大学数据挖掘期末复习

概念题